|
>>> Navigation laden |
|
|
|
Wie funktioniert ein Kaleidoskop ? |
|
Bei den zur Demonstration aufgebauten Spiegeln wurden keine Oberflächenspiegel verwendet, so sieht man die Spiegelkanten und den Unterschied Originalbild/Spiegelung besser. Durch sauber verarbeitete Oberflächenspiegel in den Kaleidoskopen wird der Spiegelspalt beinahe unsichtbar und die Spiegelungen sind kaum vom Ausgangsbild zu unterscheiden. |
|
|
| Kaleidoskope sind Illusionsgeräte, deren Aufbau aber eigentlich recht einfach ist. |
|
|
| 1 Spiegel |
|
2 Spiegel |
|
|
 |
 |
|
|
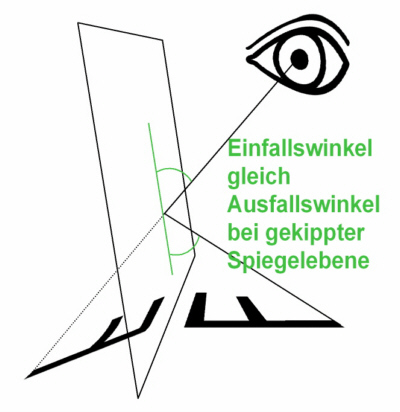
| Die einfache Reflexion: Der Spiegel steht senkrecht zur gespiegelten Fläche. Wir erinnern uns vielleicht aus der Schule: Reflexionen funktionieren nach dem Gesetz: Einfallswinkel gleich Ausfallswinkel. |
|
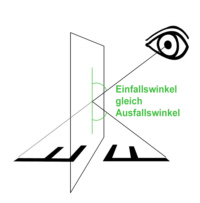 |
|
Durch den zweiten Spiegel kommt ein neues Element hinzu, jetzt Spiegelt sich das Spiegelbild im Spiegel. Während das rechte und linke "F" eine einfache Spiegelung des Originalbilds sind, ist das obere "F" durch die Spiegelung der Spiegelung entstanden, (der linke Abschnitt durch die Spiegelung des rechten im linken Spiegels - und umgekehrt). Ein 90° Winkel ergibt 4 Motive. |
|
 |
|
 |
|
|
| Verkleinert man den Spiegelwinkel auf 45°, so bekommt man mehr Motive. Ein Kreuz oder Quadrat kann sich ergeben, (Das oberste "F" ist die Spiegelung der Spiegelung der Spiegelung der Spiegelung). |
|
Ist der Winkel zwischen den Spiegeln ungenau, ist das letzte Motiv gegenüber dem Originalbild unvollständig oder teilweise doppelt dargestellt. |
|
|
| Ein geschlossenes symmetrisches Bild ergibt sich nur bei Teilungen von 360° durch eine gerade Zahl. |
|
geteilt durch 4 = 90° (4Bilder - rechts gespiegelt zu links und oben zu unten, wie Bild 2)
geteilt durch 6 = 60° (6 Bilder, Dreieck/Dreistern)
geteilt durch 8 = 45° (8 Bilder, Quadrat/Kreuz)
geteilt durch 10 = 36° (10 Bilder, Fünfeck/Fünfstern)
geteilt durch 12 = 30° (12 Bilder, Sechseck/Sechsstern)
geteilt durch 14 = 25,7° (14 Bilder, Siebeneck/Siebenstern)
geteilt durch 16 = 22,5° (16 Bilder, Achteck/Achtstern)
usw. - solange man noch in den Spiegelspalt schauen kann.
Die dritte Seite ist bei 2-spiegeligen Kaleidoskopen meist schwarz.
|
|
|
| 3 Spiegel |
|
|
|
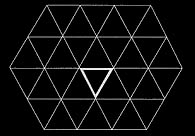
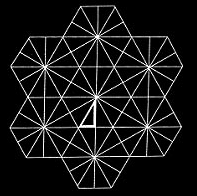
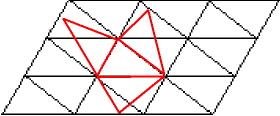
Bei drei Spiegeln spiegelt sich der Stern wiederum im gegenüberliegenden Spiegel und es entsteht ein weitläufiger Musterteppich.
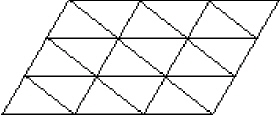
Soll dieser Musterteppich geschlossen symmetrisch sein, funktioniert das nur mit bestimmten Spiegelwinkeln. Das sind alle Dreiecke, mit denen man nahtlos eine Fläche füllen kann, die an den Spiegelachsen symmetrisch sind:
60°-60°-60° ...............................45°-45°-90° ................................30°-60°-90°
|
|
|
 |
|
|
 |
 |
 |
|
|
|
 |
|
 |
|
|
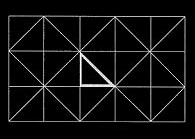
| Noch ein Beispiel zur Verdeutlichung: Man kann zwar mit jeder Form von Dreiecken eine Fläche auslegen aber an den Spiegelachsen ergibt sich hier kein symmetrisches Gegenbild. |
|
|
|
3-D Illusionen |
|
|
 |
 |
|
|
| Steht der Spiegel schräg zur gespiegelten Fläche, wird die Spiegelung im gleichen Winkel gekippt. |
|
Hier liegt ein geichseitiges Dreieck schräg in einer Spiegelecke aus drei Spiegeln, die im Winkel von 90° zueinander stehen. Durch den rechten und linken Spiegel ergibt sich eine Pyramide, durch den unteren Spiegel wird diese auch nach unten gespiegelt und die Illusion eines Oktaeders entsteht.
Übrigens ist es gar nicht möglich, diese Spiegelkonstellation zu fotografieren, ohne dass die Kamera im Bild ist. Wenn man hinein blickt, sieht man immer das eigene Auge im Zentrum, egal von welcher Richtung man schaut. Nach dem selben Prinzip funktionieren die Katzenaugen-Reflektoren: Viele kleine Kunststoff-Facetten, mit diesen Winkeln, senden das Licht immer dorthin zurück, von wo es herkommt. |
|
 |
|
|
 |
|
 |
|
|
| Dieses Bild stammt aus dem nebenstehenden Kaleidoskop mit 30°-60°-90° Winkeln, dessen Spiegel trapezförmig sind und ebenfalls in einem bestimmten Winkel zueinander gekippt sind. |
|
| 3-D Kaleidoskop ohne Gehäuse |
|
|
| Ein ausführlicher Artikel zu diesem Thema, verfasst von Jürgen Richter-Gebert von der TU München, ist zu finden unter diesem LINK >>> (er ist außerdem zu finden in dem Buch: Alles Mathematik: Von Pythagoras zu Big Data | Martin Aigner, Ehrhard Behrends | ISBN: 9783658099893) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|















